Analytic Continuation Problem

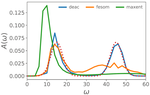
For over thirty years a long standing problem in quantum many-body physics has been to reliably extract dynamical information from imaginary time quantum Monte Carlo data. Sch"uttler and Scalapino were the first to highlight the intrinsic difficulty by using a least-squares approach. The solution which amounts to performing an inverse Laplace transform to recover spectral functions became known as a notoriously ill-posed problem. Modern techniques use Bayesian inference with regularization (maximum entropy method), stochastic optimization, and genetic algorithms to approximate suitable results. These approaches often fail for experimentally relevant data collected at finite temperatures or data containing large relative uncertainties due to statistically low sampling rates at larger imaginary time steps. Additionally, these methods are prone to large parameter sweeps and critical slowing down causing increased user input and computational effort. A new method using current evolutionary computation routines is developed to assuage these stumbling blocks. The Differential Evolution for Analytic Continuation (DEAC) algorithm is a parameter free method that uses self adaptive differential evolution to extend the domain of imaginary time density-density correlation functions and reconstruct accurate representations of dynamic structure factor spectra at zero and finite temperatures. Preliminary outcomes indicate huge speedup and resolving power over other traditional and state-of-the-art methods. I will continue algorithmic development of these techniques through hyphenated methods combining DEAC with other analytic continuation techniques to offer improved quality of spectra. Another exciting avenue for development is using a machine-learning approach extending previous work to finite temperatures.